Continuing further from our previous article part I Adding multiple Call & Put Options Payoff Functions, here are the next steps:

Step 4 - Separate the payoff functions for PUTS alone (both LONG PUT options and Short PUT options):
Considering ONLY the put options, here is how they will look. There are a total of 2 PUT positions - one $55 LONG PUT (YELLOW Payoff function) and another $50 SHORT PUT (PINK Payoff function):


Step 5 - Add all the payoff functions for PUTS alone (both LONG PUT options and SHORT PUT options):
IMPORTANT: Care should be taken that multiple PUT options should be added from the RIGHT side i.e. starting from the higher values on the horizontal axis (like +100) and then move towards the lower values of (0). This is exactly opposite to what we did for adding call options in step 3.
This is the reason why we have to separate out call options and put options. Getting this step wrong will result in errors. So make sure that you add the call options from left to right and put options from right to left.
Let's begin:
Looking at it from right side, between $100 and $55, both the PINK and YELLOW payoff functions are Zero. Hence, net sum = Zero
Between $55 and $50, the Yellow payoff function has a upward slant, while PINK payoff function is Zero. So net sum = same as that of Yello Payoff function
Between $50 and $0, the Yellow payoff function has a upward slant, while PINK payoff function has a downward slant. So both opposite slantss cancel each other and you get a net zero slant i.e. a horizontal line.
Overall sum of both put option positions is represented by GREEN colored payoff function.


Step 6 - Add the net payoff functions for PUTS & CALLS from step 3 and step 5) :
Step 3 gave us net ORANGE graph (for call options) and step 5 gave us net GREEN graph (for put options), which look as follows:

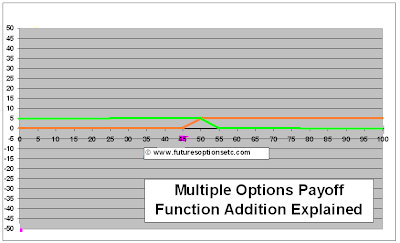
Since we have now plotted the NET payoff functions of both call and put options on one single graph, the direction of addition is no longer required. We can add these net payoff functions from any directions.
Let's begin from the left side - between $0 and $45, the call option orange graph is zero while put option green graph has a value of $5. Hence, $0 + $5 = $5 net. (PLUM colored horizontal graph between $0 and $45)

Between $45 and $50, the call option orange graph is upward slanting while put option green graph has a value of $5, hence the net sum will be (upward slant value +$5 = PLUM colored upwrd slanting graph between $45 and $50)

Similarly, $50 and $55, the call option orange graph is horizontal with value of $5 while put option green graph is downward slanting, hence the net sum will be (downward slant value +$5 = PLUM colored downward slanting graph between $50 and $55)

Between $55 and above, the call option orange graph has a value of $5 while put option green graph is zero, hence the net sum in this region is $5. (PLUM colored horizontal graph between $55 and above)


Step 7 - the last step - adjust for the net price:
Now that we have got the PLUM colored net payoff function for all the various option positions, we need to adjust for the net price we receive/pay in total.
Since we had the following positions in Microsoft Options in this example:

1. Call - Long - Strike Price of $45 - Bought at $7
2. Call - Short - Strike Price of $50 - Sold at $3
3. Put - Long - Strike Price of $55 - Bought at $8
4. Put - Short - Strike Price of $50 - Sold at $2

We received $3 +$2 = $5 from sale (short) of 2 options, while we have to pay $7 + $8 = $15 from the Buy (LONG) of 2 options. Hence, net we paid $15 - $5 = $10. (net outflow)
Hence, the PLUM colored zero priced payoff function will move downwards by an amount of $10 (as it is a net pay / outflow)
Overall, this is how it will look (BROWN Colored Payoff function with Price considered):

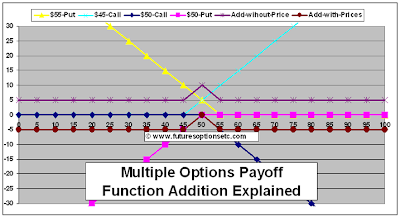
Summary of mathematics of payoff functions:
Be it any option or derivative, one needs to master the addition of payoff function which helps in understanding the profit and loss areas clearly.
The example covered above is a very good way to demonstrate what many options trader ignore. Check the BROWN colored payoff function which summarizes the profit and loss regions for these 4 option positions. The brown graph always remains below the ZERO line (below horizontal axis). The highest value it touches is Zero at the underlying price of $50. This means that irrespective of whatever happens, no way will the option trader make any profit from any movement in the price of the underlying microsoft stock. This combination will always result in a loss to the option trader.
Further add to it the option brokerage and trading commissions, this brown graph will shift further down meaning more loss. Since you are taking 4 option positions at the entry level and will have to exit all 4 later, the brokerage costs will also be higher.
Hence, it is very important to be aware about the net overall option payoff for the multiple positions one is getting into.

Video-How-to-Add-Multiple-Option-Positions-Part-1

See the next part 2 of this video at : Video-How-to-Add-Multiple-Option-Positions-Part-2
In the next article, we will see how to add payoff functions for multiple expiry dates but on the same underlying.